ピラミッドの単位は、√2：√2：√3 の直方体

人類は、「ものを数えるため言葉」として、1 から始まる正の数である整数を数字とします。古代から整数は自然数といわれていますが、彼らは整数以外の数字も知っていたから、あえて、整数を自然数としたのではないでしょうか。その答えは、ピラミッドにありました。

現代科学は、ピラミッドの構造を、キュービットという単位で構成された立方体であると説明しています。１キュービットは、0.5236ｍの立方体で、辺に４４０キュービット、２８０キュービットの高さで四角錐ということになっています。

注目するのは傾斜角度です。計算ではこのピラミッドの傾斜角度は51.83度。実際のピラミッドの傾斜角度の実測値は下記のとおりです。

①　カフラ王のピラミッド：53.16°
②　メンカウラ王のピラミッド：51.3°
③　クフ王のピラミッド：51.8°

キュービットという立方体で作られた場合に、この傾斜をどのように作ったのでしょうか。

そこで、まず、最初に、この傾斜角度をもつ直方体を考えます。その基準となるのが、√１、√２、√３という無理数です。計算結果は下記のとおりです。

④　√１：√１：√２の場合　50.81度
⑤　√２：√２：√３の場合　54.65度

①のピラミッドは⑤に近似していて、②と③のピラミッドは、④に近似していないでしょうか。

これを踏まえて、①の√１：√１の面を底辺とする直方体を中心から螺旋状に並べていきます。辺が１７列で正方形ができて、頂上までは９段の構造物ができます。



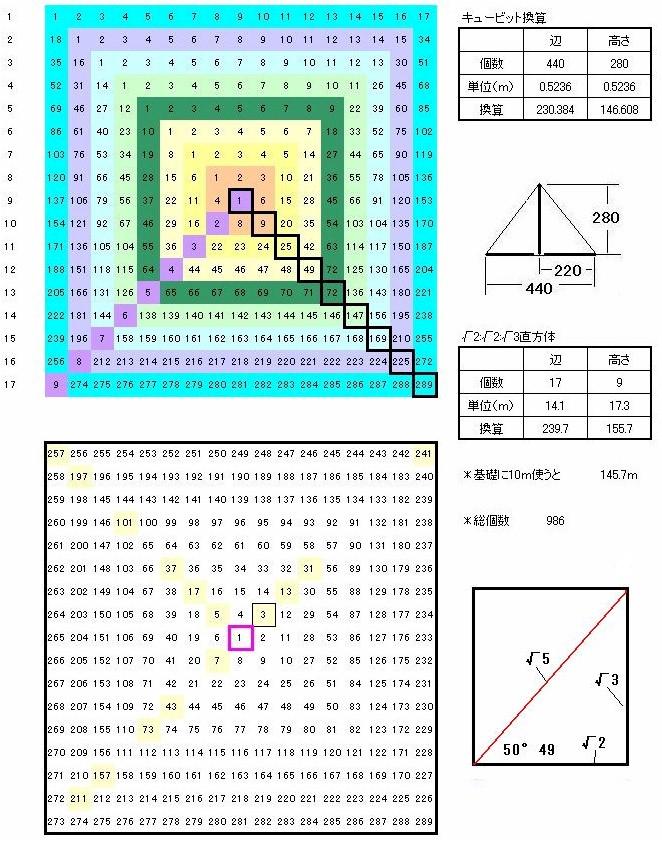
ただ、基本的には、上の図のように直方体を並べた構造物は地球ではすぐに崩れるでしょう。古代の人々は、なんども崩れるピラミッドを見て、構造計算しやすい自然数を取り入れたのではないでしょうか。

無理数を使う文明は、地球の歴史では存在しません。ピラミッドはモニュメント（記念建物）であると考えると、これは、地球外生命体の文化であると考えれば合理的です。

地球外生命体の文化というか科学の象徴がピラミッドであり、この科学は無理数を使用していたとすれば、ピラミッドの謎もとけるでしょう。

現代科学は、重力も光合成も、そしてピラミッドすら解明できていないという事実を再認識するべきです。科学は、重力を自然法則として受け入れ、質量という概念をつくり、無理数である素数を無視しました。素数は科学では神話になったのです。

しかし、無理数を探求することではなく、自然数という存在に、問題の本質があったのではないでしょうか。つまり、見方を変えて、無理数が数の基本ではないかと考えるのです。つまり、１，２，３と数えずに、√１、√２、√３、として三進法で考える。

この問題定義に対する答えがピラミッドではないでしょうか。